ewewe

Revisori: Sara Sottile, Matteo Talluri.

Figura 1: quadrato di lato 1.

Immaginiamo di voler colorare il quadrato, i.e. coprire la sua area, in modo tale che si colori prima una metà, poi la metà della metà rimanente, e così via, come rappresentato nella figura 2.

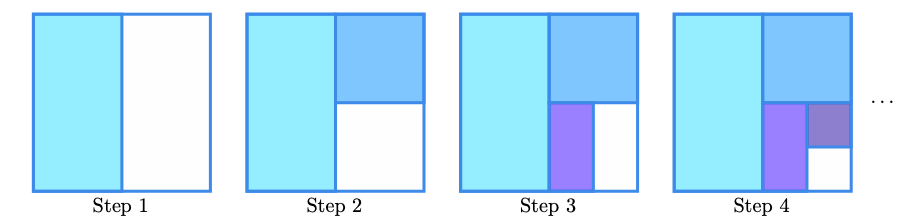
Figura 2: esaustione del quadrato.

Ad ogni passo, rimane sempre una porzione di quadrato che non viene colorata, ma l’area di questa porzione si dimezza ad ogni passo. Intuitivamente, risulta chiaro che occorrono infiniti passi affinché il quadrato sia completamente riempito, e che alla fine di questo processo infinito l’area colorata sarà

(1)

Il metodo appena descritto è noto come metodo di esaustione. Nel seguito, cf. (5) e proposizione 3, daremo una dimostrazione formale dell’identità (1).

La teoria delle serie numeriche comincia già nell’antica Grecia, quando il più grande matematico del mondo antico, Archimede di Siracusa (287 a.C.-212 a.C.), utilizza il metodo di esaustione per calcolare l’area sottesa a un ramo di parabola. Per molto tempo l’idea che una somma infinita di numeri potesse produrre un valore finito fu considerata assurda. Abbiamo già citato il paradosso, dovuto al filosofo Zenone di Elea (489 a.C-431 a.C), noto come “paradosso di Achille e la tartaruga”. Achille “pié veloce” vuole raggiungere una tartaruga (nota per essere lenta) che si trova a una certa distanza da lui. I due cominciano a muoversi nello stesso istante. Achille, per raggiungerla, arriva con un balzo nel punto in cui è partita la tartaruga, la quale però, nel frattempo, si è mossa e nel momento in cui Achille ha compiuto il suo balzo, la tartaruga ha percorso una certa distanza. Allora, Achille, con un balzo, percorre quella stessa distanza. Tuttavia, nel frattempo, la tartaruga si è mossa ancora in avanti. Ripetendo questo ragionamento all’infinito, concludiamo che Achille non raggiungerà mai la tartaruga. Questo paradosso può essere superato facendo uso delle serie numeriche, cf. esercizio 1.

I primi tentativi di formalizzare il concetto di somma infinita di numeri risalgono al XVII secolo e sono attribuiti a James Gregory (1638-1695), Colin Maclaurin (1698-1746) e Brook Taylor (1685-1731). Leonhard Euler (1707-1783), con il suo lavoro sulle serie ipergeometriche, formalizza le prime proprietà delle serie numeriche, lavoro che fu poi completato da Johann Carl Friedrich Gauss (1777-1855), che ad oggi è considerato il padre della moderna teoria. Tra i matematici che hanno dato maggiore contributo alla teoria possiamo citare Leibniz, Cauchy, Dirichlet, Abel, Raabe, Kummer e molti altri.

La conoscenza delle serie numeriche costituisce la base per lo sviluppo in serie di potenze delle funzioni, cominciato in primo luogo con gli sviluppi intorno un punto ad opera di McLaurin e Taylor.

In conclusione, il concetto di serie numerica (insieme a quello di integrale¹) è stato da sempre oggetto di studi e rappresenta quindi uno dei cardini dell’analisi matematica, trovando applicazioni in molti ambiti scientifici.

Nella sezione 1 diamo le prime definizioni ed enunciamo i risultati che seguono immediatamente da queste, e successivamente elenchiamo le principali proprietà delle serie numeriche. Nella sezione 2 introduciamo due tipi fondamentali di serie, quelle geometriche e quelle telescopiche. Successivamente, nelle sezioni 3 e 4, enunciamo e dimostriamo i più noti criteri di convergenza, prima per serie a termini non negativi, e poi per serie qualunque. A seguire, la sezione 5 è dedicata allo studio del prodotto di due serie, mentre nella sezione 6 vengono enunciati e dimostrati i principali risultati sul riordinamento di una serie. Le ultime due sezioni, 7 e 8, contengono una raccolta di esercizi, suddivisi per argomento e ordinati per difficoltà. La prima di tali sezioni è la più ampia, ed è completa di soluzione.

Infine, nella sezione Appendice A discutiamo i prodotti infiniti, mentre nella sezione Appendice B approfondiamo lo studio della serie armonica, definendo la costante di Eulero-Mascheroni.

1. Si può dimostrare che questi due concetti sono strettamente collegati, ma ciò esula dallo scopo di queste note. ↩

(1)

cioè la somma dei primi termini della successione, al variare di .

Definizione 1 (serie numerica). La serie associata alla successione si definisce come segue:

(2)

Se il limite delle somme parziali (2) esiste finito, diciamo che la serie associata alla successione è convergente. Se, invece, tale limite esiste infinito, diciamo che la serie associata alla successione è divergente. Infine, se tale limite non esiste, diciamo che la serie associata alla successione è indeterminata.

Notiamo che la notazione non deve essere interpretata come una somma di infiniti termini, ma come il limite delle somme parziali, cf. (2).

Dalla definizione 1 segue che nel caso in cui la serie sia non convergente possiamo distinguere tre casi:

• • Il limite esiste e ;

• • Il limite esiste e ;

• Il limite non esiste.

Nel primo caso si dice che la serie diverge positivamente, nel secondo caso si dice che diverge negativamente e nel terzo caso, come già detto, che è indeterminata.

Infine, diciamo che è il termine generale della serie .

Osservazione 1. La scelta di far partire la serie da è puramente arbitraria. Avremmo potuto scegliere un qualunque , una successione , e definire la serie associata

(3)

in modo analogo².

Osservazione 2. La definizione 1 si estende naturalmente al caso in cui è una successione di numeri complessi. Diremo allora che la serie

converge a se vale

(4)

mentre diremo che la serie diverge a se la successione è illimitata. Infine, diremo che la serie è indeterminata se non esiste alcun tale che valga (4).

2. Si noti che tale scrittura (3) non è affatto più generale di (2), in quanto si può ottenere una dall’altra con il cambio di indici . ↩

Esempio di serie convergente

Anticamente si pensava che sommando infiniti termini positivi, il risultato fosse necessariamente . Se, per somme infinite, intendiamo il limite delle somme parziali, cf. definizione 1, ciò non è vero, come mostra il seguente esempio.

Consideriamo la serie a termini positivi

Rappresentando i termini della serie come lunghezze, e suddividendo un segmento di lughezza unitaria in metà, e poi una delle metà ottenute di nuovo a metà, e così via, si vede facilmente che³

Passando al limite per si ha:

(5)

Abbiamo dunque dimostrato che la serie converge al valore .

Esempio di serie divergente

Abbiamo visto che una serie si dice divergente se la successione delle somme parziali di è divergente.

Per esempio:

Esempio di serie indeterminata

Abbiamo visto che una serie si dice indeterminata se la successione delle somme parziali di è indeterminata.

Per esempio, consideriamo la serie . Le successione delle somme parziali vale:

Dato che le sottosuccessioni di indice pari e dispari della successione delle somme parziali hanno limite diverso, non ha limite, ovvero la serie è indeterminata.

3. Tale fatto si può formalizzare facilmente con il principio di induzione. ↩

Proposizione 1 (condizione necessaria per la convergenza). Sia una serie convergente. Allora, il suo termine generale è infinitesimo, i.e. si ha

Dimostrazione. Sia , dove è definita da (1). Notiamo che

(6)

Passando al limite per in (6), e sfruttando i teoremi algebrici sui limiti, cf. [9, pag. 49], si ha

dove in abbiamo usato l’ipotesi di convergenza della successione .

Esempio 1. Studiamo il carattere della seguente serie

(7)

Osserviamo che

dunque la serie non converge perché non è soddisfatta la condizione necessaria alla convergenza, i.e. il termine generale non è infinitesimo. Seguirà dal lemma 1 che, poiché la serie data è a termini positivi, essa diverge positivamente.

Terminologia. Una serie si dice serie a termini di segno costante se la successione è a termini di segno costante, i.e. (serie a termini non negativi) oppure (serie a termini non positivi), altrimenti si dice serie a termini di segno variabile.

Una serie della forma con si dice serie a segno alterno.

Prima di enunciare il prossimo risultato, richiamiamo la seguente definizione.

Definizione 2 (proprietà definitive). Sia una successione e sia una proprietà sull’insieme . Diciamo che la successione gode definitivamente della proprietà se esiste tale che gode della proprietà per ogni . In formule:

Dimostrazione. Per fissare le idee, consideriamo una serie a termini definitivamente non negativi, e sia tale che . Dimostriamo che la successione delle somme parziali, cf. (1), è definitivamente non decrescente. Infatti, per ogni , si ha

Dunque .

Allora, per il teorema delle successioni monotone, cf. [4, pag. 71], si ha che

(8)

Se la serie di partenza è a termini definitivamente non positivi, la dimostrazione è analoga. Osserviamo, infine, che rimuovendo la parola definitivamente, cioè, assumendo la serie a termini non negativi (risp. non positivi), si conclude che il limite in (8) è non negativo (risp. non positivo).

Osservazione 3. Dalla dimostrazione precedente, deduciamo che una serie a termini di segno definitivamente costante converge se e solo se la successione delle somme parziali è limitata.

Il carattere di una serie non cambia se non vengono considerati un numeri finito di termini. Prima di enunciare questo risultato, ricordiamo un fatto elementare sulle successioni.

Dimostrazione. Sia tale che per ogni si ha . Distinguiamo due casi.

• • Primo caso. Supponiamo che esista . Allora, dai teoremi algebrici sui limiti, cf. [9, pag. 49], si ha

    

• Secondo caso. Supponiamo che non esista . Se per assurdo esistesse , dai teoremi algebrici sui limiti, avremmo

  

  cioè esisterebbe in contrasto con l’ipotesi.

Corollario 1. Sia una successione. Per ogni , le serie

hanno lo stesso carattere.

Dimostrazione. Le somme parziali

differiscono per una costante, infatti

Dunque, per il lemma 2 le due successioni delle somme parziali (e quindi, per definizione, le due serie) hanno lo stesso carattere.

Corollario 2. Siano due successioni che coincidono definitivamente. Allora, le serie

hanno lo stesso carattere.

Dimostrazione. Basta considerare tale che per ogni e applicare il corollario 1 con .

Proposizione 2 (criterio di Cauchy per le serie). La serie converge se e solo se:

(9)

Dimostrazione. Sia la successione delle somme parziali. Ricordiamo⁴ che una successione converge se e solo se è di Cauchy⁵, cf. [3], [11]. Quindi, converge se e solo se

(10)

Per possiamo scrivere

(11)

da cui ponendo si ottiene la seguente condizione, equivalente alla convergenza della serie,

(12)

4. Questo fatto è noto come completezza dei numeri reali. ↩

5. Una successione è di Cauchy se ↩

Lemma 3. Sia una serie convergente. Allora, per ogni , la serie converge, e si ha

(13)

Se, invece, la serie diverge, allora diverge per ogni .

Dimostrazione. Sia definita da (1) e notiamo che

(14)

Passando al limite per in (14), e sfruttando l’ipotesi che esiste finito, si ottiene la prima parte della tesi. Per la seconda parte, il procedimento è analogo. Notiamo che, se , abbiamo per ogni , e quindi la serie corrispondente a è nulla.

Il prossimo risultato mette in relazione la serie corrispondente alla somme di due successioni, con la somma delle serie corrispondenti.

Lemma 4. Siano date le serie e . Allora,

• • se entrambe le serie convergono, anche la serie converge e si ha

    

 

• se entrambe le serie divergono positivamente (risp. negativamente), oppure se una diverge positivamente (risp. negativamente) e l’altra converge, allora la serie diverge positivamente (risp. negativamente).

Dimostrazione. Consideriamo le successioni delle somme parziali:

Per la proprietà commutativa della somma, si ha:

Passando al limite per , e applicando le proprietà dei limiti, si ottiene la tesi.

Definizione 3 (progressione geometrica). Una successione si dice progressione geometrica se è costante il rapporto tra un termine della successione e il suo precedente (quando tale termine è definito). Tale rapporto viene detto ragione della progressione geometrica.

Segue subito dalla definizione⁶ che, detta la ragione di una successione geometrica , si ha

(15)

6. Applicando, ad esempio, il principio di induzione. ↩

Definizione 4 (serie geometrica). Una serie si dice serie geometrica di ragione se la successione è una successione geometrica di ragione e . In altre parole, è una serie geometrica se è della forma⁷

(16)

per qualche .

---

7. Seppure non è definito, in questo contesto si suole abusare di notazione e intendere che anche se . ↩

Di seguito determiniamo il carattere della serie geometrica (16) al variare di , dimostrando prima un risultato utile a tale scopo.

Lemma 5 (somma geometrica). Sia . Allora, vale che:

Dimostrazione. Sia . Il caso è immediato, in quanto si ottiene sommando lo stesso termine (i.e. 1) volte, quindi . Notiamo che, per ogni , si ha

da cui

cioè

La seguente proposizione è immediata conseguenza del lemma 5.

Proposizione 3 (carattere serie geometrica). Sia . La serie geometrica di ragione vale

(17)

Dimostrazione. Per determinare il carattere della serie utilizziamo la definizione, cf. definizione 1. Possiamo cioè calcolare il limite la successione delle somme parziali utilizzando il lemma 5.

Se , abbiamo:

(18)

da cui, ricordando che per , otteniamo:

Osservazione 4. La serie geometrica si può facilmente calcolare a partire da un qualunque , sfruttando la proposizione 3, ovvero possiamo calcolare

Se si ha che per ogni

Approfondimento. Un modo per visualizzare la serie geometrica consiste nel considerare la seguente figura:

Figura 3: visualizzazione della serie geometrica.

Costruiamo i rettangoli (in celeste, cf. figura 3) di base e altezza con . Osserviamo che tutti i triangoli rettangoli (in arancione, cf. figura 3) sono simili tra di loro perché i cateti sono in rapporto , poiché si ha:

Notiamo che la lunghezza di del segmento è dato dalla serie geometrica di ragione :

Poiché i triangoli e sono simili, otteniamo la relazione

ovvero

Definizione 5 (serie telescopica). Una serie si dice telescopica (risp. non banale) se esiste una successione tale che

(19)

Con il termine serie telescopica, solitamente si sottointende una serie telescopica non banale.

Data una serie telescopica, cf. (19), la successione delle somme parziali ha un’espressione esplicita in termini della successione .

Lemma 6 (somma telescopica). Sia una successione. Allora, vale che

(20)

Dimostrazione. Basta notare che tutti i termini della somma compaiono due volte con il segno opposto, tranne il primo e l’ultimo:

(21)

Proposizione 4 (carattere serie telescopica). Sia una serie telescopica, allora vale:

(22)

Dimostrazione. Dal lemma 6, si ha

Osservazione 5. Si poteva equivalentemente definire una serie telescopica di termine come una serie tale per cui per qualche successione . Ponendo , si vede che le due scritture sono equivalenti. Segue immediatamente dalla proposizione 4 che, nel caso in cui esista, si ha

(23)

L’utilità di una o dell’altra scrittura dipende dal contesto.

Osservazione 6. Segue immediatamente dal lemma 6. e dalla proposizione 4 che

(24)

nel caso in cui quest’ultimo limite esista.

(25)

diverge positivamente.

Infatti, applicando la (17) con , otteniamo che la serie diverge a .

Esempio 3. Dimostriamo che la serie

(26)

è convergente, e calcoliamone la somma.

Applicando la (17), otteniamo

Esempio 4. La serie

(27)

è indeterminata.

Infatti, applicando la (17) con , otteniamo che la serie è indeterminata.

Esempio 5 (serie di Mengoli). Dimostriamo che la serie

(28)

è convergente, e calcoliamone la somma.

Questa serie è telescopica. Infatti, possiamo riscrivere il termine generale come

Applicando (23), otteniamo

Esempio 6. La serie

(29)

è divergente.

Infatti, notiamo che la serie data è telescopica in quanto possiamo riscrivere il termine generale come

Applicando (22), otteniamo

Esercizio 1. Consideriamo il paradosso di Achille e la tartaruga spiegato nell’introduzione. Supponiamo che la distanza iniziale della tartaruga sia di metri, la velocità della tartaruga sia di metro al secondo e quella di Achille il doppio di quella della tartaruga. Dopo quanti metri Achille raggiunge la tartaruga? In quanto tempo?

Svolgimento. La velocità di Achille è di metri al secondo. Dunque, poiché al tempo “” la distanza è “”, al tempo “” Achille raggiunge la posizione iniziale della tartaruga. Nel frattempo, la tartaruga ha percorso “”. Per raggiungere la posizione in cui si trova la tartaruga al tempo , Achille impiega “”, e in quel lasso di tempo la tartaruga percorre “”. Ragionando per induzione, e utilizzando la proposizione 3, si trova che la distanza che Achille deve percorrere per raggiungere la tartaruga è

Il tempo che impiega è di

Teorema 1 (criterio del confronto). Siano due successioni numeriche tali che definitivamente vale . Allora, si ha:

1. 1. (30)

 

1. (31)

Dimostrazione. Sia tale che

(32)

e definiamo

Per il corollario 1 abbiamo che le serie

convergono se e solo se i limiti delle successioni (che esistono per il lemma 1) sono finiti, rispettivamente. Dato , sommando ambo i membri di (32) per da a , otteniamo che , e dunque

(33)

Allora, se il limite di destra è finito, è finito anche il limite di sinistra, da cui otteniamo (30). Se, infine, il limite di sinistra è infinito, lo è anche il limite di destra, da cui otteniamo (31).

Esempio 7. Consideriamo la serie

e dimostriamo che essa è convergente utilizzando il criterio del confronto.

Notiamo che la serie è a termini positivi, quindi possiamo applicare il criterio del confronto. Operando il cambiamento di indice nella sommatoria, si ha

Notiamo che, poiché per ogni , si ha

dunque, poiché la serie

è convergente, cf. esempio 5, concludiamo che la serie data è convergente per il criterio del confronto.

Teorema 2 (criterio del confronto asintotico). Siano due successioni a termini definitivamente positivi e tale che definitivamente. Supponiamo che

Si ha che

1. 1. Se e , allora ;

 

1. 1. se e , allora ;

 

1. se , allora se e solo se .

Dimostrazione.

1. 1. Per ipotesi sappiamo che

      

      Posto , otteniamo

      

      da cui, per il criterio del confronto, cf. teorema 1, si ha la tesi.

1. 1. Per ipotesi sappiamo che

      

      Posto , si ha che

      

      da cui, per il teorema del confronto, cf. teorema 1, si ha la tesi.

1. Per ipotesi sappiamo che

   

   cioè

   

   Posto , si ha

   (34)

   Se , per la prima disequazione di (34) e per il criterio del confronto, cf. teorema 1, si ha che . Altrimenti, se , per la seconda disequazione di (34) e per il teorema del confronto, cf. teorema 1, si ha che .

Esempio 8. Consideriamo la serie

e dimostriamo che essa è convergente utilizzando il criterio del confronto asintotico.

Notiamo che la serie è a termini positivi, quindi possiamo applicare il criterio del confronto asintotico. Ricordiamo che si ha

dunque, poiché la serie

è convergente, cf. esempio 7, concludiamo che la serie data è convergente per il criterio del confronto asintotico.

Teorema 3 (criterio di condensazione di Cauchy). Sia una successione a termini positivi non crescente, ovvero

Allora, le serie

hanno lo stesso carattere.

Dimostrazione. Dall’ipotesi di non crescenza della successione , otteniamo che

(35)

in quanto ognuno dei termini della somma (35) è minorato da .

Fissato , abbiamo dunque

(36)

dove nella prima disuguaglianza abbiamo trascurato i termini con e nell’ultima disuguaglianza abbiamo applicato (35). Passando al limite nella (36) e ricordando, cf. Lemma 1, che il limite esiste, otteniamo che

(37)

Analogamente alla (35), otteniamo che

(38)

Fissato , abbiamo dunque

(39)

dove nella prima disuguaglianza abbiamo aggiunto a destra i termini con

\displaystyle \sum_{n=0}^{+\infty }2^na_{2^n} \displaystyle \sum_{n=1}^{+\infty }a_n\alpha \in \mathbb{R}

S_\alpha+\infty\alpha \leq 0+\infty\alpha < 0\alpha = 0+\infty\alpha \leq 0\alpha > 0S_\alpha

q = 2^{1-\alpha}|q| < 1\alpha > 1S_\alpha\alpha > 1\alpha \leq 1\alpha, \beta \in \mathbb{R}

\beta=0\alpha < 0\alpha = 0\beta > 0S_{\alpha,\beta}+\infty\alpha > 0\beta\alpha = 0\beta > 0S_{\alpha,\beta}

0 < \alpha < 12^{1-\alpha} > 1\alpha = 1\beta\beta > 1\alpha > 1\beta > 0(2^{1-\alpha})^nq = 2^{1-\alpha} < 1S_{\alpha,\beta}

\alpha > 1\beta \in \mathbb{R}\alpha = 1\beta > 1S_{\alpha,\beta}+\infty

\alpha = 1\beta \leq 1\alpha < 1\beta \in \mathbb{R}\displaystyle \sum_{n=1}^{+\infty}a_n

\ell\in [0,1)\ell\in(1,+\infty] \ell=1

{\ell\in[0,1)}

a_n >0\forall\, n \geq N_\varepsilon

\varepsilon_0= \dfrac{1-\ell}{2}>0

\forall \,n\geq N_{\varepsilon_0}

M<1\displaystyle \sum_{n=1}^{+\infty}a_n{\ell\in(1,+\infty]}\ell>1n_0 > 0 \forall \,n\geq n_0,\,\, \dfrac{a_{n+1}}{a_n}>1\{ a_n \}\displaystyle \sum_{n=1}^{+\infty}a_n\left\{ a_n \right\}{\ell=1}\{a_n\}_{n\in \mathbb{N}}, \{a_n’\}_{n\in \mathbb{N}}

a_n \to + \inftyn \to + \infty\{ a_n \}\{ a’_n \}\ell=1\{ a_n \}_{n \in \mathbb{N}}\subset \mathbb{R}

\ell <1 \ell>1

\displaystyle \lim_{n\to +\infty}\dfrac{a_{n+1}}{a_n}=1^+\ell>1\{ a_n \}

a_n\coloneqq \dfrac{n!}{n^n}

\displaystyle \sum_{n=1}^{+\infty}a_n

\displaystyle \limsup_{n \to +\infty} \dfrac{a_{n+1}}{a_n}<1\displaystyle\liminf_{n \to +\infty} \dfrac{a_{n+1}}{a_n}>1a_{n+1}>a_n

\displaystyle \sum_{n=1}^{+\infty}a_n

\displaystyle \sum_{n=1}^{+\infty}a_n

\ell\in [0,1)\ell\in(1,+\infty] \ell=1

{\ell\in[0,1)}

\varepsilon_0=\dfrac{1-\ell}{2}M \coloneqq \ell+\varepsilon_0\forall \, n\geq N_{\varepsilon_0}

M<1\displaystyle \sum_{n=1}^{+\infty}a_n{\ell\in(1,+\infty]}

\ell = +\infty\ell\in(1,+\infty)\varepsilon_0=\dfrac{\ell-1}{2} C=\ell-\varepsilon_0N=N_{\varepsilon_0}

C>1\displaystyle \sum_{n=1}^{+\infty}a_n{\ell=1}\{a_n\}_{n\in \mathbb{N}}, \{a_n’\}_{n\in \mathbb{N}}

\displaystyle \sum_{n=1}^{+\infty}a_n

\displaystyle \limsup_{n \to +\infty} \sqrt[n]{a_n} <1\displaystyle \limsup_{n \to +\infty} \sqrt[n]{a_n} >1a_n\geq 1

\{ a_{2k} \}_{k \in \mathbb{N}}\{ a_{2k+1} \}_{k \in \mathbb{N}}\{ a_n \}_{n\in \mathbb{N}}

\ell=\ell’

a_{n}

\ell >0\varepsilon\ell-\varepsilon>0N=N_\varepsilonn = N

n

\ell=00

\ell > \varepsilon

\ell=0

\ell=0\forall\, n \geq M

\varepsilon\eta

\{x_{n}\}_{n\in\mathbb{N}}, \{y_{n}\}_{n\in\mathbb{N}} \subset \mathbb{R}\left\{ y_{n} \right\}

n \to + \infty

\ln(0)\coloneqq -\infty

\displaystyle \lim_{n\to +\infty} \frac{a_{n+1}}{n}2

\{ a_n \}

\{ a_n \}_{n\in \mathbb{N}}f:[1,+\infty) \rightarrow \mathbb{R}f(n) = a_n n\in\mathbb{N}\displaystyle \int\limits_{1}^{+\infty}f(x)\,{\rm d}x\displaystyle \sum_{n=1}^{+\infty}a_n

S_N \coloneqq \displaystyle\sum_{n=1}^{N}a_n, \; N \in \mathbb{N},\{ a_n \}f

n1N

S_N

N\to +\infty

S=\displaystyle\sum_{n=1}^{+\infty}a_n

f[ 1,6]S_6-a_1S_5

n_0f:[ n_0, +\infty) \to \mathbb{R}f(n)=a_n \; \forall n \in \mathbb{N} \displaystyle \sum_{n=1}^{+\infty} a_n \displaystyle \int_{n_0}^{+\infty}f(x)\,{\rm d}x.

a_n= n \ln n\ln^2(\ln n)n\geq 3

f_1,f_2,f_3: [3,+\infty)\to (0,+\infty)

f_1f_2f_3f

y=\ln(\ln x){\rm d}y= \dfrac{{\rm d}x}{x\ln x}

\displaystyle \sum_{n =1}^{+\infty} a_n

\displaystyle \ell\in(1,+\infty]\displaystyle\ell \in [-\infty,1)\displaystyle \ell=1

{\ell\in(1,+\infty)}\varepsilon >0 N_\varepsilon>0

\varepsilon_0\coloneqq\ell-1>0\forall\,n> N_{\varepsilon_0}\quad a_n>0

\{n a_n\}\varepsilon_10<\varepsilon_1<\ell-1k \coloneqq \ell – \varepsilon_1 -1>0N\coloneqq N_{\varepsilon_1}\forall\,n >N

\{ n a_n \}\displaystyle \sum_{n=1}^{+\infty}a_n{\ell =+\infty}k>0, \, N \in \mathbb{N}{\ell \in(-\infty,1)}\varepsilon>0N_\varepsilon>0

\varepsilon_0\coloneqq 1-\ell>0N\coloneqq N_{\varepsilon_0}

\{na_n\}

\displaystyle \sum_{n=1}^{+\infty}a_n{\ell =-\infty} N \in \mathbb{N}{\ell=1}\{a_n\}\{a^\prime_n\}

a_n=\dfrac{1}{n}a^\prime_n=\dfrac{1}{n\ln^2 n}

\{ a_n \}

\{ a’_n \}

\ell=1\ell=1

f: (0,+\infty) \to \mathbb{R}, \; f(x)=x\ln^2(x)

n \in \mathbb{N}\eta_n\in(0,1)

\ln^2(n)

\dfrac{a_{n}}{a_{n+1}}-10n\to+\infty\dfrac{a_{n+1}}{a_n}

\displaystyle \sum_{n =1}^{+\infty} a_n

\displaystyle\liminf_{n\to + \infty}b_n>1\displaystyle\limsup_{n \to + \infty}b_n<1\displaystyle \sum_{n =1}^{+\infty} a_n

\ell \in [-\infty,-1)\ell \in (-1,+\infty]\ell=-1

{\ell \in\mathbb{R}}

\forall \, n > N_\varepsilon

\ell >-1\varepsilon>0\varepsilon – \ell <1\varepsilon-\ell\leq1\ell> -1\displaystyle \sum_{n=N_\varepsilon+1}^{+\infty}a_n \ell <-1\varepsilon>0-\varepsilon – \ell >1-\varepsilon-\ell>1\ell<-1\displaystyle \sum_{n=N_\varepsilon+1}^{+\infty}a_n {\ell=+\infty}

a_n{\ell=-\infty}

a_n{\ell=-1}\{a_n\}\{a^\prime_n\}

a_n=\dfrac{1}{n}a^\prime_n=\dfrac{1}{n\ln^2 n }

\{ a_n \}_{n \in \mathbb{N}} \subset \mathbb{R} \displaystyle \sum_{n=0}^{+\infty} a_n

\displaystyle \sum_{n=0}^{+\infty} a_n\{ a_n \}_{n \in \mathbb{N}} \subset \mathbb{R}\displaystyle \sum_{n=0}^{+\infty} a_n

\displaystyle \sum_{n=0}^{+\infty} a_n\{ a_n \}_{n \in \mathbb{N}} \subset \mathbb{C}

\vert \cos \left( n\right)\vert \leq 1n\in\mathbb{N}

n\to+\infty

\sum_{n=1}^{+\infty}\dfrac{n^2}{n^4+7n}

\{a_n\}_{n \in \mathbb{N}}\subset \mathbb{R}

\{a_n\} \lim\limits_{n\rightarrow +\infty}a_n = 0\displaystyle \sum_{n=0}^{+\infty}(-1)^n a_n

\{ a_n \}

n_0n \geq n_0a_{n+1}\leq a_nn_1>n_0a_{n_1}<0\displaystyle \lim_{n \to + \infty}a_n\leq a_{n_1}<0\{ a_n \}\displaystyle S_n \coloneqq \sum_{k = 0}^{n}(-1)^k a_k, \; n \in \mathbb{N}n

n

na_{2n}\geq a_{2n+1}\geq a_{2n+2}\{S_{2n+1}\}_{n\in \mathbb{N}}\{S_{2n}\}_{n\in \mathbb{N}}\{ S_{2n+1} \}

\lim\limits_{n \to + \infty}a_n=0

\{a_n\}\displaystyle \sum_{n=0}^{+\infty}(-1)^na^\prime_na^\prime_n=-a_n\forall \, \varepsilon>0 \quad \exists N_1, N_2>0\left( n>N_1 \implies \left \vert S_{2n}-\ell_1\right \vert <\varepsilon \right)\left( n>N_2 \implies \left \vert S_{2n+1}-\ell_2\right \vert <\varepsilon \right)\ell_1=\ell_2N_\varepsilon=\max\{ N_1,N_2 \}

a_n = \dfrac{1}{n}

\sqrt[n]{n}\geq 1 \quad \forall\, n \in \mathbb{N}a_n\coloneqq \sqrt[n]{n}-1

\displaystyle \left(1+\frac{1}{n}\right)^n\leq e < 3

\left\{ \dfrac{1}{\sqrt{n}} \right\}_{n\geq 1}

a_nb_n\{ a_n \}_{n \in \mathbb{N}}, \{ b_n \}_{n \in \mathbb{N}} \subset \mathbb{R}\{ B_n \}\{ b_n \}

n,m \in \mathbb{N}m>n

\clubsuit\diamondsuit\{ a_n \}_{n \in \mathbb{N}}, \{ b_n \}_{n \in \mathbb{N}} \subset \mathbb{R}

\{a_n\}_{n \in \mathbb{N}}\lim\limits_{n\rightarrow +\infty}a_n = 0 \{B_n\}_{n \in \mathbb{N}}\left\{ b_n \right\} \displaystyle \sum_{n=0}^{+\infty}a_n b_n

\{a_n\}\{a_n\}B_n \coloneqq \displaystyle \sum_{k=0}^n b_kn \in \mathbb{N}

n>N_\varepsilonp> 0

\{ B_n \}\{ a_n \}a_n>0 n>N_\varepsilonN_\varepsilon\displaystyle \sum_{n=0}^{+\infty}a_nb_n\{a_n\}\displaystyle \sum_{n=0}^{+\infty}a^\prime_nb_na^\prime_n=-a_n \displaystyle \sum_{n=1}^{+\infty} (-1)^na_n, \{a_n\}

b_n=(-1)^n, \; n \in \mathbb{N}\{ b_n \}

\displaystyle \sum_{n=0}^{+\infty}(-1)^n a_n

a_nb_na_n = \dfrac{1}{\sqrt{n}+1}b_n = \sin(n)\{a_n\}\displaystyle B_n \coloneqq \sum_{k=0}^{n}b_k = \sum_{k=0}^n \sin(k)2\sin\left(\dfrac{1}{2}\right)\forall \, n \in \mathbb{N}

\clubsuit

\diamondsuit

a_nb_na_n = \dfrac{1}{n}b_n = \cos(n)\{a_n\}\displaystyle B_n \coloneqq \sum_{k=0}^{n}b_k = \sum_{k=0}^n \sin(k)2\sin\left(\dfrac{1}{2}\right)\forall \, n \in \mathbb{N}

\clubsuit

\diamondsuit

\alpha\in (0,+\infty)\left\{\dfrac{1}{n^\alpha}\right\}\alpha \in (0,+\infty)

i

\clubsuitx \in \mathbb{C}\{ B_n \}

a_n\alpha \in (0,+\infty)-1ii^2=-1\{ a_n \}_{n \in \mathbb{N}}, \{ b_n \}_{n \in \mathbb{N}} \subset \mathbb{R}

\{a_n\}\displaystyle \sum_{n=0}^{+\infty}b_n\displaystyle \sum_{n=0}^{+\infty}a_n b_n

\{a_n\}

\{ a_n \}

B_n \coloneqq \displaystyle \sum_{k=0}^n b_kn \in \mathbb{N}N_\varepsilon

\{ B_n \}M

n>N_\varepsilonp> 0

B_{n+p} a_{n+1}|B_k|\{ a_n \}_{n>N_{\varepsilon}}N_\varepsilon\displaystyle \sum_{n=0}^{+\infty}a_nb_n\{a_n\}\displaystyle \sum_{n=0}^{+\infty}a^\prime_nb_na^\prime_n=-a_n\{ a_n \}\{ b_n \}a\coloneqq \lim\limits_{n\to +\infty}a_n

a_n-ab_n\alpha_n\beta_nb_n

a_nb_na_n = \arctan(n)b_n = \dfrac{\sin(n)}{n} \{ a_n \}f:\mathbb{R} \to \mathbb{R}, \; f(x)=\arctan(x)0\leq \arctan(x)< \dfrac{\pi}{2}x \geq 0 \displaystyle \sum_{n=1}^{+\infty}b_n \left\{ \dfrac{\arctan(n)}{n} \right\}f: (0,+\infty) \to \mathbb{R}, \; f(x)= \dfrac{\arctan(x)}{x}

\alpha\in \mathbb{R}\cos(\pi n)=(-1)^nn \in \mathbb{N}

\left\{\dfrac{1}{n^\alpha+\left(-1\right)^n}\right\}n\to+\infty

\{ a_n \}\alpha>0\alpha\leq 0\{ b_n \}\displaystyle \sum_{n=2}^{+\infty}\dfrac{1}{n^{2\alpha}}\displaystyle \sum_{n=2}^{+\infty}\dfrac{1}{n^{2\alpha}}\alpha >\dfrac{1}{2}\{ a_n \}\{ b_n \}

\alpha \in \left(\dfrac{1}{2},+\infty\right)

\alpha\in \mathbb{R}n\to+\infty

a_nb_nn \to + \infty

b_n\{ a_n \}\{ b_n \}

\alpha\in (0,+\infty)

n\to+\infty

a_n\left\{\left(1+\dfrac{1}{n}\right)^{-n}n^{-\alpha}\right\}\alpha>0\alpha \in(0,+\infty)b_n

\alpha \in\left(\dfrac{1}{2},+\infty\right)

\alpha \in \left(\dfrac{1}{2},+\infty\right)

\alpha\in (0,+\infty)n\to+\infty

a_n\alpha \in (0,+\infty)b_n\alpha \in \left(\dfrac{1}{2},+\infty\right)\displaystyle \sum_{n=1}^{+\infty}\dfrac{1}{n^{2\alpha}}S_\alpha\alpha \in \left(\dfrac{1}{2},+\infty\right)

\alpha\in (0,+\infty)n\to +\infty

a_n\alpha \in (0,+\infty)b_n

b_n\alpha \in \left(\dfrac{1}{2},+\infty\right)S_\alpha\alpha \in \left(\dfrac{1}{2},+\infty\right)\displaystyle \sum_{k=0}^{n}a_{k}\displaystyle \sum_{k=0}^{m}b_{k}

n,m \to + \infty\forall\, k \geq 0

\displaystyle \sum_{k=0}^{+\infty}a_{k}\displaystyle \sum_{k=0}^{+\infty}b_{k}\ast

\astf: \mathbb{N}\to \mathbb{R}, \;g: \mathbb{N}\to \mathbb{R}f\ast g

f(n)\coloneqq a_{n}, \;g(n)\coloneqq b_{n}

a_n

x \in \mathbb{R}x,y \in \mathbb{R}

x \in \mathbb{R}e^x

A \coloneqq \displaystyle \sum_{n=0}^{+\infty}a_{n}, \; B \coloneqq \sum_{n=0}^{+\infty}b_{n}

\displaystyle \sum_{n=0}^{+\infty}a_{n}\left\{ A_n \right\}\left\{ B_n \right\}\left\{ C_n \right\}\displaystyle \sum_{n=0}^{+\infty}a_{n}\displaystyle \sum_{n=0}^{+\infty}b_{n}\displaystyle \sum_{n=0}^{+\infty}c_{n}\left\{ \beta_n \right\}

B_n \to Bn \to + \infty

a_i0\leq i \leq na_iB0\leq i \leq nA_nB \to ABn \to + \infty

\left\{ a_0\beta_n + a_1\beta_{n-1}+ \dots + a_n\beta_0 \right\}M>0

\varepsilon>0n_0>0

\left\{ \beta_n \right\}n_1>0

n \geq n_0+n_1

\left\{ a_0\beta_n + a_1\beta_{n-1}+ \dots + a_n\beta_0 \right\}\displaystyle A \coloneqq \sum_{n=0}^{+\infty}a_{n}, B \coloneqq \sum_{n=0}^{+\infty}b_{n}

\displaystyle A\coloneqq \sum_{n=0}^{+\infty}a_{n}\displaystyle \left\{ A_{n} \right\}

n \in \mathbb{N}\displaystyle x_{n}\coloneqq \sum_{k=0}^{n}A_{k}y_{n}\coloneqq n

n \in \mathbb{N}\left\{ x_n \right\}, \; \left\{ y_n \right\}

n \in \mathbb{N}\left\{ x_n \right\}, \; \left\{ y_n \right\}

n \in \mathbb{N}

m\coloneqq ky_k

\displaystyle C\coloneqq \sum_{n=0}^{+\infty}c_{n}\displaystyle c_{n}=\sum_{k=0}^{n}a_{k}b_{n-k} \quad \forall\, n \in \mathbb{N}\left\{ A_{n} \right\}, \left\{ B_{n} \right\}, \left\{ C_{n} \right\}\displaystyle\sum_{n=0}^{+\infty}a_{n}, \sum_{n=0}^{+\infty}b_{n}

n \geq 1

n \in \mathbb{N}\alpha_{n}\coloneqq A_{n}-A, \;\beta_{n}\coloneqq B_{n}-B

n\to +\infty

M>0|\beta_{n}|\leq Mn \in \mathbb{N}\{\beta_{n}\}

\displaystyle x_{n}\coloneqq \sum_{k=0}^{n}|\alpha_{k}|y_{n}\coloneqq n

\displaystyle \sum_{n=0}^{+\infty}a_n

\zeta: (1,+\infty) \to \mathbb{R}

A_\infty

n \rightarrow + \infty

n

n \rightarrow +\infty

A_nna_1, a_2 \in \mathbb{R}

\displaystyle \sum_{k = 0}^{ +\infty} b_k\displaystyle\sum_{k = 0}^{ +\infty} a_k\sigma: \mathbb{N} \to \mathbb{N}b_k = a_{\sigma(k)}

kk’b_k=a_{k’}\sigma={\rm id}_{\mathbb{N}}\displaystyle \sum_{k = 0}^{+ \infty} b_k\displaystyle\sum_{k = 0}^{ \infty} a_k{\sigma}\displaystyle\sum_{k = 0}^{+ \infty} a_k\displaystyle\sum_{k = 0}^{+ \infty} b_k\sigma^{-1}\displaystyle \sum_{k = 0}^{+ \infty} a_k\displaystyle \sum_{k = 0}^{+\infty} b_k

\{ S_n \}S

\{ \tilde{S}_n \}

sTT

T_{3n}\displaystyle \left( 1 + \frac{1}{3} – \frac{1}{2} \right)=\frac{5}{6}T_nn\to +\infty

T\dfrac{5}{6}T \neq SS=\ln 2\displaystyle\sum_{k = 0}^{+\infty} a_k\displaystyle \sum_{k = 0}^{+\infty} b_kb_n

S =\displaystyle \sum_{k = 0}^{+\infty} b_k T =\displaystyle \sum_{k = 0}^{+\infty} a_kS_nT_nn\in\mathbb{N}a_{\sigma(1)} + \cdots + a_{\sigma(n)} T

n \to +\infty

T_n

n \to +\infty

S = T\displaystyle \sum_{k = 0}^{+\infty} a_k\displaystyle\sum_{k = 0}^{+\infty} b_k\displaystyle \sum_{k = 0}^{+\infty} b_k

|a_k||b_k|\displaystyle \sum_{k = 0}^{+\infty} |b_k|\displaystyle \sum_{k = 0}^{+\infty} |a_k|\displaystyle \sum_{k = 0}^{+\infty} b_k

b_k =|b_k| – (|b_k| – b_k)\displaystyle \sum_{k = 0}^{+\infty}|b_k| \displaystyle \sum_{k = 0}^{+\infty} (|b_k| – b_k) |b_k|(|b_k| – b_k) (|b_k| – b_k) (|a_k| – a_k)

\displaystyle \sum_{k = 1}^{ +\infty} a_k \alpha \in \mathbb{R} \cup \{ \pm \infty\}\displaystyle \sum_{k = 1}^{ +\infty} b_k \alpha

\alpha \in \R \cup \{ \pm \infty \}\alpha\geq 0,\alpha<0

S_n\pm \infty

\alpha \in (0,+\infty)\alphaa_n^+n_1

m_1

\{ n_i \}, \{ m_i\}n_{i+1}>n_im_{i+1}>m_ii>0

\alphaT_n, \;n>0\{ a_k \}_kpp\leq n\{ T_n-\alpha \}

\{ a_n \}\alpha\alpha=+\infty\{ n_i \}, \{ m_i\}n_{i+1}>n_im_{i+1}>m_ii>0

ia_{m_{i}}<1

T_nnT_n>1mT_m<-1

|\sin(x)|\leq 1x \in \mathbb{R}

\dfrac{1}{4}<1

b_n

\left\{\left(1-\dfrac{1}{n^3}\right)^{-n^3}\right\}e

\alpha \in (3,+\infty)

\alpha \in (0,3)

\alpha=3

\displaystyle \lim_{n\to +\infty}\left(1-\dfrac{1}{n^3}\right)^{n^3}=e^{-1}\neq 0\alpha \in (0,3]\alpha \in (3,+\infty)

n \rightarrow +\infty

\sqrt{5n+4}<2^n n\geq 2n=1n \geq 2

\displaystyle \sum_{n=2}^{+\infty}a_nn\rightarrow +\infty

a_n

n \rightarrow +\infty

\{b_n\}_{n\in \mathbb{N}}k>0n \rightarrow +\infty

n\to+\infty

2\alpha\alpha \in \left(\dfrac{1}{2},+\infty\right)\alpha \in \left(\dfrac{1}{2},+\infty\right)

n\to+\infty

2-\alpha

\alpha \in (-\infty,1)\alpha \in [1,+\infty)

\alpha \in (-\infty,1]\alpha \in (1,+\infty)

\alpha \in (-\infty,1]\alpha \in (1,+\infty)

n\to+\infty

\alpha=\dfrac{1}{12}O(1)n^{-1}

n\to+\infty

\alpha \in (1,+\infty)\alpha \in (1,+\infty)

n\to+\infty

\alpha \in (1,+\infty)

a_n

a_n

\ell = 4 > 1

a_n

a_n

\ell<1

a_n

0<\alpha<\dfrac{4}{e}\alpha>\dfrac{4}{e^2}\alpha =\dfrac{4}{e}

\alpha= \dfrac{4}{e}

\alpha \in \left(0,\dfrac{4}{e}\right)

a_n

0<\alpha<\dfrac{4}{e^2}\alpha>\dfrac{4}{e^2}\alpha =\dfrac{4}{e^2}

n\to + \infty

n\rightarrow+\infty

\alpha= \dfrac{1}{2}\alpha \in \left(0,\dfrac{4}{e^2}\right)

\ell=1\alpha=17>1

\displaystyle \lim_{n\to+\infty}2^{\frac{2}{n}}=1\displaystyle \lim_{n\to+\infty}\left(1+\dfrac{1}{n^2}\right)^{n^2}=e

\left\{ \dfrac{1}{n\ln n \ln^\alpha \left(\ln n \right)} \right\}

\alpha>1

\dfrac{e^n}{1+e^{2n}}n \in \mathbb{N}

\displaystyle \sum_{n=0}^{+\infty}\dfrac{e^{n}}{1+e^{2n}}<+\infty

\displaystyle \sum_{n=1}^{+\infty}\dfrac{n!}{n^n}

\displaystyle \sum_{n=1}^{+\infty}\dfrac{1}{4^n+5^n}

n\in \mathbb{N}n!!\coloneqq n(n-2)!$, dove si pone per convenzione $(-1)!!\coloneqq 10!!\coloneqq 1\{ a_n \}

\dfrac{e}{\alpha}-1>0\dfrac{e}{\alpha}-1<0\alpha=e[0\cdot +\infty]\alpha=e

\alpha\in \left(0,e\right) \displaystyle\sum_{n=1}^{+\infty}\dfrac{n!}{n^n}\alpha\in [e,+\infty) \displaystyle\sum_{n=1}^{+\infty}\dfrac{n!}{n^n}\alpha=e

\clubsuit-\alpha<-1\alpha>1\alpha=1\alpha=1n \to + \infty

\alpha=1

\alpha>3

\forall\,n \in \mathbb{N}\quad (1+1/n)^n<3

n

n

n\to+\infty

n\to+\infty

\alpha\in (1,+\infty)\alpha \in (1,+\infty)\alpha\alpha \in (0,1)\alpha \in (0,1)

\alpha>2\alpha \in (0,2)

\alpha \in (0,2)

\alpha\in (0,2)\alpha=0\alpha=2

\alpha \in (0,1)

\alpha=0\alpha=2

\alpha<0\alpha>0\alpha=0

\displaystyle \lim_{n\to+\infty} \left(n^2+3\right)=+\infty \alpha \in(-\infty,0)

\alpha<1\alpha>1\alpha=1

n\to+\infty

\alpha=1\alpha=1

n\to+\infty

\{ a_n \}

\alpha\in \left(\dfrac{1}{3},+\infty\right)\alpha \in \left(\dfrac{1}{3},+\infty\right)

f: \mathbb{R}\setminus \{0\} \to \mathbb{R},\; f(x)=\dfrac{x^2+4x+8}{x^3+2x^2+7x}

\{ a_n \}

f:(1,+\infty) \to \mathbb{R},\; f(x)=\left(1-\dfrac{1}{x}\right)^{x\ln x }

a_{n+1}\leq a_n

\alpha \in \mathbb{R}\{a_n\}

\alpha <1\{a_n\}\alpha \geq1\{ a_n \}

\sum_{n=1}^{+\infty}a_nb_n

\{a_n\}\displaystyle\left\{ \sum_{k=1}^{n}b_k \right\}

\{a_n\}\{a_n\}\displaystyle \left\{ \sum_{k=1}^{n} \cos k\right\}\displaystyle \sum_{n=0}^{+\infty}a_k \sin k \{a_n\}

n\to+\infty

n\to+\infty

\alpha>0

\alpha \in \mathbb{R}{\alpha \in (-\infty ,0]}n\to+\infty

-2-\alpha>1\alpha<-3{\alpha \in (0,+\infty)}n\to+\infty

\alpha \in (-\infty,-3)\cup (0,+\infty)

{\alpha \in \left(-\infty,\,4\right).}

{\alpha =4.}

{\alpha\in \left(4,\,+\infty\right).}

\alpha \in [0,1)\alpha \in (1,+\infty)\alpha=1

n\to +\infty

\alpha \in [0,1)

{\alpha \in(0,1)}n\to+\infty

\alpha\in(0,1)\alpha\in(0,1){\alpha=1}

{\alpha\in(1,+\infty)}n\to+\infty

\dfrac{1}{\alpha}\in(0,1)\alpha > 1

\alpha\in \mathbb{R}

n\to +\infty

0<b\leq a

0<a<b

\min\{a,b\}<\dfrac{\pi}{2}

f: \mathbb{R} \to \mathbb{R}, \; f(x)=\sin x[-1,1]

\sin(1) \approx 0.84 < 1

a_nb_n

n \rightarrow +\infty

1{\alpha \in \left(-\infty,10\right)}

3{\alpha=10}n\to+\infty

\alpha=103{\alpha \in (10,+\infty)}

\alpha \in (10,+\infty)\alpha \in \mathbb{R}\setminus\{10\}

\alpha \in \left(\dfrac{1}{2},+\infty\right)\forall\,a,b,c>0\quad \log_a(c)=\log_b(c)/\log_b(a)

x \in (0,1)n\to+\infty

x \in (0,1)x=1

x>1n\to +\infty

x>1x \in (0,1) \cup (1,+\infty)

nn \mapsto n+1

n\to+\infty

a_nb_nc_n

n\to+\infty\forall\, n,k \in \mathbb{N}k\leq n\displaystyle \binom{n}{k}\coloneqq \frac{n!}{k!(n-k)!}

\forall\, n,k \in \mathbb{N}k\leq n\displaystyle \binom{n}{k}\coloneqq \frac{n!}{k!(n-k)!}n\to+\infty

M \in \left(1,+\infty\right) \cap \mathbb{N}M \geq 1

n\to+\infty

f: \mathbb{R} \to \mathbb{R}, \; f(x)=\sin x[0,1]

\{ a_n \}\{ b_n \}

\left\{\dfrac{1}{\left(n^2+1\right)\arctan \left(n\right)}\right\}

n\to+\infty

\alpha \neq \dfrac{5}{24}\alpha < \dfrac{5}{24}\alpha >\dfrac{5}{24}\alpha =\dfrac{5}{24}

\alpha \in \mathbb{R}\{ a_n \}

\alpha \in \mathbb{R}

\alpha< 0\left\{ \dfrac{2}{n^{\alpha} }\right\}\{ a_n \}\alpha=02-\sin(x)\geq 1 \quad \forall \, x \in \mathbb{R}a_n\geq nn \geq 1\{ a_n \}0<\alpha<1/2\left\{ \dfrac{2}{n^{\alpha} }\right\}\{ a_n \}\alpha=1/2

1/2<\alpha<1

\{ a_n \}\alpha-12\alpha-2\alpha=1

\{ a_n \}\alpha>1\{ a_n \}\alpha<1a_n\alpha\geq 1\alpha=1\alpha>1

\alpha>21<\alpha\leq 2\alpha \in \{1\}\cup(2,+\infty)

n^{\left(n^{n-1}\right)} \geq n^{n+1}

n \geq 1

*** QuickLaTeX cannot compile formula:
<a name="id3505261959"></a><span class="ql-right-eqno"> (274) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-de3f1ade266aaf8a1d9db5447a49a1cb_l3.svg" height="48" width="691" class="ql-img-displayed-equation " alt="\begin{equation*} \dfrac{\sqrt{2\pi n!}}{n^{\left(n^n\right)}}\left(\dfrac{n!}{e}\right)^{n!}= \dfrac{\sqrt{2\pi n!}}{n^{\left(n^n\right)}} \cdot \dfrac{\left(n!\right)^{n!}}{e^{n!}}=\exp\left(n!\ln\left(n!\right)+\dfrac{1}{2}\ln\left(2\pi\right)+\dfrac{1}{2}\ln\left(n!\right)-n^n\ln\left(n\right)-n!\right). \end{equation*}" title="Rendered by QuickLaTeX.com"/>
Notiamo che
<a name="id3005145895"></a><span class="ql-right-eqno"> (275) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-6dddf9188dc44096c39b7d10ad849591_l3.svg" height="97" width="585" class="ql-img-displayed-equation " alt="\begin{equation*} \begin{aligned} \lim_{n\to+\infty}\dfrac{n!\ln\left(n!\right)}{n^n\ln \left(n\right)}&=\lim_{n\to+\infty}\dfrac{\sqrt{2\pi n}\left(\ln\left(\sqrt{2\pi n}\right)+n\ln\left(n\right)-n+\ln\left(1+o\left(1\right)\right)\right)}{e^n\ln \left(n\right)(1+o(1))}=\\ &=\lim_{n\to +\infty}\dfrac{\sqrt{2\pi n}\left(n\ln \left(n\right)\right)}{e^n\ln\left(n\right)}\left(1+o\left(1\right)\right)=0, \end{aligned} \end{equation*}" title="Rendered by QuickLaTeX.com"/>
dunque, da (\ref{eq1:misti:es58}), (\ref{eq2:misti:es58}) e (\ref{eq3:misti:es58}), otteniamo che
<a name="id666270295"></a><span class="ql-right-eqno"> (276) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-e93e337a9aff60312ea5d9b4fdb3182d_l3.svg" height="39" width="416" class="ql-img-displayed-equation " alt="\begin{equation*} \dfrac{\left(n!\right)!}{n^{\left(n^n\right)}}= \exp\left[-n^n\ln\left(n\right)\,(1+o(1))\right], \qquad \text{per}\,\,n\to+\infty. \end{equation*}" title="Rendered by QuickLaTeX.com"/>
Infine, confrontiamo il termine generale della serie data con quello di una serie di cui è nota la convergenza, ad esempio una serie armonica generalizzata di esponente maggiore di 1, cf. lemma <a id="def-Lemma 7-ref" href="#def-Lemma 7">7</a>:
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-64dd7d7acc4cc67ed5f26385352093a2_l3.svg" height="86" width="331" class="ql-img-displayed-equation " alt="\[\lim_{n\to+\infty}\dfrac{\dfrac{\left(n!\right)!}{n^{\left(n^n\right)}}}{\left( \dfrac{1}{n^2} \right)} =\lim_{n\to+\infty} \dfrac{e^{-n^n\ln n\,\left(1+o\left(1\right)\right) }}{\left( \dfrac{1}{n^2} \right)}=0.\]" title="Rendered by QuickLaTeX.com"/>
Concludiamo, per il criterio del confronto asintotico, che la serie data converge.
[/learn_more]
<a id="Esercizio 77" class="bright-blue-link" href="#Esercizio 77"></a>
<div style="padding: 10px; background-color: #ffe4ce;"><strong style="color: #000000;">Esercizio 77</strong> <img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-47c5ad7bd42823dbf18c33db4aa83798_l3.svg" class="ql-img-inline-formula " alt=" (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)" title="Rendered by QuickLaTeX.com" height="20" width="124" style="vertical-align: -5px;"/>. Calcolare la somma della seguente serie:
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-5d1dcc1d525e2dda52d525875c5e53dc_l3.svg" height="51" width="199" class="ql-img-displayed-equation " alt="\[S=\sum_{n=1}^{+\infty}\dfrac{1}{n\left(n+1\right)\left(n+2\right)} .\]" title="Rendered by QuickLaTeX.com"/></div>
[learn_more caption="Svolgimento."]
Decomponiamo in fratti semplici il termine generale:
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-bb1db766b427415b33c4193b547449b5_l3.svg" height="43" width="449" class="ql-img-displayed-equation " alt="\[\dfrac{1}{n\left(n+1\right)\left(n+2\right)}=\dfrac{A}{n}+\dfrac{B}{n+1}+\dfrac{C}{n+2}\quad \text{con}\,\,A,B,C\in \mathbb{R},\]" title="Rendered by QuickLaTeX.com"/>
da cui
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-0cc868a6f411e1295b3b4a79fceaf152_l3.svg" height="95" width="517" class="ql-img-displayed-equation " alt="\[\begin{aligned} \dfrac{1}{n\left(n+1\right)\left(n+2\right)}&=\dfrac{A\left(n^2+3n+2\right)+B\left(n^2+2n\right)+C\left(n^2+n\right)}{n\left(n+1\right)\left(n+2\right)}=\\ &=\dfrac{\left(A+B+C\right)n^2+\left(3A+2B+C\right)n+2A}{n\left(n+1\right)\left(n+2\right)}. \end{aligned}\]" title="Rendered by QuickLaTeX.com"/>
Otteniamo il sistema
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-097310f52d18f8903e1b0e8ec3764751_l3.svg" height="98" width="331" class="ql-img-displayed-equation " alt="\[\begin{cases} A+B+C=0\\ 3A+2B+C=0\\ 2A=1 \end{cases} \quad \iff \quad \begin{cases} A=\dfrac{1}{2}\\ B=-1\\ C=\dfrac{1}{2}. \end{cases}\]" title="Rendered by QuickLaTeX.com"/>
Quindi
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-632e88d1158f68f964e3387a7a63e519_l3.svg" height="43" width="664" class="ql-img-displayed-equation " alt="\[\begin{aligned} &\dfrac{1}{n\left(n+1\right)\left(n+2\right)}=\dfrac{1}{2n}-\dfrac{1}{n+1}+\dfrac{1}{2\left(n+2\right)}=\dfrac{1}{2}\left(\dfrac{1}{n}-\dfrac{1}{n+1}\right)+\dfrac{1}{2}\left(\dfrac{1}{n+2}-\dfrac{1}{n+1}\right). \end{aligned}\]" title="Rendered by QuickLaTeX.com"/>
Pertanto, dal fatto che la somma è telescopica, cf. lemma <a id="def-Lemma 6-ref" href="#def-Lemma 6">6</a>, otteniamo
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-fc3c6c04ac15a2fae18da0a24097922f_l3.svg" height="103" width="674" class="ql-img-displayed-equation " alt="\[\begin{aligned} S&=\lim_{N\to+\infty}\sum_{n=1}^{N}\dfrac{1}{n\left(n+1\right)\left(n+2\right)}=\lim_{N\to+\infty}\sum_{n=1}^{N}\dfrac{1}{2}\left[\left(\dfrac{1}{n}-\dfrac{1}{n+1}\right)+\left(\dfrac{1}{n+2}-\dfrac{1}{n+1}\right)\right]=\\ &=\lim_{N\to+\infty}\dfrac{1}{2}\left(1-\dfrac{1}{N+1}-\dfrac{1}{2}+\dfrac{1}{N+2}\right)=\dfrac{1}{2}\left(1-\dfrac{1}{2}\right)=\dfrac{1}{4}. \end{aligned}\]" title="Rendered by QuickLaTeX.com"/>
[/learn_more]
<a id="Esercizio 78" class="bright-blue-link" href="#Esercizio 78"></a>
<div style="padding: 10px; background-color: #ffe4ce;"><strong style="color: #000000;">Esercizio 78</strong> <img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-47c5ad7bd42823dbf18c33db4aa83798_l3.svg" class="ql-img-inline-formula " alt=" (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)" title="Rendered by QuickLaTeX.com" height="20" width="124" style="vertical-align: -5px;"/>. Calcolare la somma della seguente serie:
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-02559f0c0237db7b9d3e30a04994c1e4_l3.svg" height="51" width="127" class="ql-img-displayed-equation " alt="\[S=\sum_{n=3}^{+\infty}\dfrac{1-\sqrt{2}}{\sqrt{2^n}} .\]" title="Rendered by QuickLaTeX.com"/></div>
[learn_more caption="Svolgimento."]
Ricordando i risultati sulla serie geometrica, cf. proposizione <a id="def-Proposizione 3-ref" href="#def-Proposizione 3">3</a> e osservazione <a id="def-Osservazione 4-ref" href="#def-Osservazione 4">4</a>, segue che
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-b0bece2640b3aea92ef14fcd5595aa0f_l3.svg" height="88" width="713" class="ql-img-displayed-equation " alt="\[S=\left(1-\sqrt{2}\right)\sum_{n=3}^{+\infty}\left(\dfrac{1}{\sqrt{2}}\right)^{n}=\left(1-\sqrt{2}\right)\left(\dfrac{\left(\dfrac{1}{2\sqrt{2}}\right)}{1-\dfrac{1}{\sqrt{2}}}\right)=\left(1-\sqrt{2}\right)\left(\dfrac{1}{2\sqrt{2}}\right)\left(\dfrac{\sqrt{2}}{\sqrt{2}-1}\right)=-\dfrac{1}{2}.\]" title="Rendered by QuickLaTeX.com"/>
[/learn_more]
<a id="Esercizio 79" class="bright-blue-link" href="#Esercizio 79"></a>
<div style="padding: 10px; background-color: #ffe4ce;"><strong style="color: #000000;">Esercizio 79</strong> <img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-47c5ad7bd42823dbf18c33db4aa83798_l3.svg" class="ql-img-inline-formula " alt=" (\bigstar\bigstar\largewhitestar\largewhitestar\largewhitestar)" title="Rendered by QuickLaTeX.com" height="20" width="124" style="vertical-align: -5px;"/>. Calcolare la somma della seguente serie:
<span class="ql-right-eqno"> (277) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-13ceecb69b04c03060ae4b1ab992838a_l3.svg" height="54" width="193" class="ql-img-displayed-equation " alt="\begin{equation*} S \coloneqq \sum_{n=1}^{+\infty}\ln\left(\dfrac{\left(n+1\right)^2}{n\left(n+2\right)}\right). \end{equation*}" title="Rendered by QuickLaTeX.com"/></div>
[learn_more caption="Svolgimento."]
Ricordando i risultati sulle somme telescopiche, cf. lemma <a id="def-Lemma 6-ref" href="#def-Lemma 6">6</a> e proposizione <a id="def-Proposizione 4-ref" href="#def-Proposizione 4">4</a>, si ha:
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-b8ed52216820bed64ecc3938805c900b_l3.svg" height="267" width="511" class="ql-img-displayed-equation " alt="\[\begin{aligned} S&=\sum_{n=1}^{+\infty}\left(2\ln\left(n+1\right)-\ln\left(n\right)-\ln\left(n+2\right)\right)=\\ &=\sum_{n=1}^{+\infty}\Big[\left(\ln\left(n+1\right)-\ln\left(n\right)\right)-\left(\ln\left(n+2\right)-\ln\left(n+1\right)\right)\Big]=\\ &=\lim_{N\to+\infty}\sum_{n=1}^{N}\Big[\left(\ln\left(n+1\right)-\ln\left(n\right)\right)-\left(\ln\left(n+2\right)-\ln\left(n+1\right)\right)\Big]=\\ &=\lim_{N\to+\infty}\Big[\big( \ln(N+1)-\ln1 \big)-\left( \ln \big(N+2\big)-\ln 2 \right)\Big]=\\ &= \lim_{N\to+\infty} \left( \ln\left( \dfrac{N+1}{N+2}\right) + \ln 2\right)=\ln 2. \end{aligned}\]" title="Rendered by QuickLaTeX.com"/>
[/learn_more]
<a id="Esercizio 80" class="bright-blue-link" href="#Esercizio 80"></a>
<div style="padding: 10px; background-color: #ffe4ce;"><strong style="color: #000000;">Esercizio 80</strong> <img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-32e12e009d8d089dbc826e478e820a31_l3.svg" class="ql-img-inline-formula " alt=" (\bigstar\bigstar\bigstar\largewhitestar\largewhitestar)" title="Rendered by QuickLaTeX.com" height="20" width="124" style="vertical-align: -5px;"/>. Calcolare la somma della seguente serie:
<span class="ql-right-eqno"> (278) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-cd2f0253bb2cfb194da164b1cd2cf3a8_l3.svg" height="51" width="239" class="ql-img-displayed-equation " alt="\begin{equation*} S\coloneqq \sum_{n=1}^{+\infty}\arctan\left(\dfrac{1}{n^2+n+1}\right). \end{equation*}" title="Rendered by QuickLaTeX.com"/></div>
[learn_more caption="Svolgimento."]
Osserviamo che
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-4cead8b54d273ff1073a582becaa32fd_l3.svg" height="43" width="211" class="ql-img-displayed-equation " alt="\[\dfrac{1}{n^2+n+1}= \dfrac{(n+1)-n}{1+ (n+1)n}.\]" title="Rendered by QuickLaTeX.com"/>
Ponendo
<a name="id1102877242"></a><span class="ql-right-eqno"> (279) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-a5464439893c529bc011a51c1b36a34a_l3.svg" height="17" width="273" class="ql-img-displayed-equation " alt="\begin{equation*} \tan\alpha \coloneqq n+1 \qquad \mbox{e} \qquad \tan\beta\coloneqq n, \end{equation*}" title="Rendered by QuickLaTeX.com"/>
abbiamo
<a name="id1019152770"></a><span class="ql-right-eqno"> (280) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-bcff4a0e2ec7a0748518744f9d90c7aa_l3.svg" height="41" width="341" class="ql-img-displayed-equation " alt="\begin{equation*} \dfrac{1}{n^2+n+1}= \dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}=\tan\left(\alpha-\beta\right), \end{equation*}" title="Rendered by QuickLaTeX.com"/>
dove, nell'ultima uguaglianza, abbiamo usato la formula di somma e sottrazione per la tangente.
Dalle equazioni (\ref{eq0:misti:es76}) e (\ref{eq1:misti:es76}), otteniamo che
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-02cd48665f798879d8f8ba2cb8070109_l3.svg" height="43" width="451" class="ql-img-displayed-equation " alt="\[\arctan\left(\dfrac{1}{n^2+n+1}\right)=\alpha - \beta= \arctan\left(n+1\right)-\arctan n,\]" title="Rendered by QuickLaTeX.com"/>
dunque la serie data è telescopica, cf. definizione <a id="def-Definizione 5-ref" href="#def-Definizione 5">5</a>.
Abbiamo dunque, cf. proposizione <a id="def-Proposizione 4-ref" href="#def-Proposizione 4">4</a>, che
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-432cc9c1e14580da262cb2f21e989e79_l3.svg" height="51" width="646" class="ql-img-displayed-equation " alt="\[\begin{aligned} &S=\sum_{n=1}^{+\infty}\left(\arctan\left(n+1\right)-\arctan n\right)=\left( \lim_{n\to+\infty}\arctan\left(n\right) \right)-\arctan 1= \dfrac{\pi}{2}-\dfrac{\pi}{4} =\dfrac{\pi}{4}. \end{aligned}\]" title="Rendered by QuickLaTeX.com"/>
[/learn_more]
<h3>Un esercizio difficile</h3>
Di seguito, proponiamo un problema di difficile risoluzione, proposto sulla rivista
``American Mathematical Monthly''<a id="footnote-24-ref" class="bright-blue-link" href="#footnote-24"><sup class="small-sup">24</sup></a>, cf. [<a id="footnote-8-ref" class="bright-blue-link" href="#footnote-8">8</a>], da O. Furdui and A. Sintamarian (Romania).
Il lettore coraggioso può provare a risolverlo autonomamente, ma sottolineiamo che tale esercizio è stato inserito come lettura piacevole, più che come sfida ardua.
Il sito <a class="bright-blue-link" href="https://quisirisolve.dvasata.com" target="_blank" rel="noopener">Qui Si Risolve</a> ha proposto le seguenti due soluzioni, che fanno uso di strumenti elementari della teoria delle serie, trattati in questa dispensa.
Ringraziamo gli autori delle soluzioni, che potete trovare, insieme a ulteriori approfondimenti sull'esercizio, elencati in <a class="bright-blue-link" href="https://quisirisolve.dvasata.com/problem-solving/american-mathematical-monthly/solution-to-problem-12215-09-o-furdui-and-a-sintamarian-romania/" target="_blank" rel="noopener">Furdui and A. Sintamarian (Romania)</a>.
<hr />
<ol start="24">
 	<li id="footnote-24"><i>Mensile statunitense in cui vengono proposti, da chiunque voglia, problemi di difficile risoluzione. La rivista pubblica periodicamente le migliori soluzioni ricevute.</i> <a class="backlink" href="#footnote-24-ref">↩</a></li>
</ol>
<a id="Esercizio 81" class="bright-blue-link" href="#Esercizio 81"></a>
<div style="padding: 10px; background-color: #ffe4ce;"><strong style="color: #000000;">Esercizio 81</strong> <img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-fc7bf217e278a967950f2d81aed07d69_l3.svg" class="ql-img-inline-formula " alt=" (\bigstar\bigstar\bigstar\bigstar\bigstar)" title="Rendered by QuickLaTeX.com" height="20" width="124" style="vertical-align: -5px;"/>. Calcolare
<span class="ql-right-eqno">   </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-2af81aab842f1f5293df266166a4f7a1_l3.svg" height="51" width="410" class="ql-img-displayed-equation " alt="\[I=\sum_{n=1}^{+\infty}\left(\left(\dfrac{1}{n^2}+\dfrac{1}{\left(n+2\right)^2}+\dfrac{1}{\left(n+4\right)^2}+\dots\right)-\dfrac{1}{2n}\right).\]" title="Rendered by QuickLaTeX.com"/></div>
[learn_more caption="Svolgimento."]
Notiamo che la serie data è a termini non negativi. Infatti, consideriamo la seguente identità, che segue dalla teoria delle serie telescopiche, cf. proposizione <a id="def-Proposizione 4-ref" href="#def-Proposizione 4">4</a>:
<a name="id1377376844"></a><span class="ql-right-eqno"> (281) </span><span class="ql-left-eqno">   </span><img src="https://quisirisolve.dvasata.com/wp-content/ql-cache/quicklatex.com-105e47e4c7a9003cf9434f43d9f154f6_l3.svg" height="52" width="273" class="ql-img-displayed-equation " alt="\begin{equation*} \frac{1}{n} = \sum\limits_{k=0}^{+\infty}\left(\frac{1}{n+2k}-\frac{1}{n+2(k+1)}\right). \end{equation*}" title="Rendered by QuickLaTeX.com"/>
Allora, per ogni

*** Error message:
Two \documentclass or \documentstyle commands.
leading text: \documentclass{
Missing $ inserted.
leading text: ...atex.com-de3f1ade266aaf8a1d9db5447a49a1cb_
Bad math environment delimiter.
leading text: ...isplayed-equation " alt="\begin{equation*}
Missing \endgroup inserted.
leading text: ...n\left(n\right)-n!\right). \end{equation*}
\begin{document} ended by \end{equation*}.
leading text: ...n\left(n\right)-n!\right). \end{equation*}
Missing $ inserted.
leading text: ...n\left(n\right)-n!\right). \end{equation*}
Extra \endgroup.
leading text: ...n\left(n\right)-n!\right). \end{equation*}
Missing $ inserted.
leading text: ...atex.com-6dddf9188dc44096c39b7d10ad849591_
Bad math environment delimiter.
leading text: ...isplayed-equation " alt="\begin{equation*}

n \geq 1

I

1/(n+k)^2(n, k)n+k1 \leqslant n \leqslant Nk \geqslant 0

\ell\leq N\ell(n,k)1 \leqslant n \leqslant Nk \geqslant 0

nNk\geq 0n\leq \ellk=\ell -nn>\ellk\geq 0k=\ell-n<0I_11/\ell^2\ell\leq N\elln=1,\dots,\ell\ell>N1/\ell^2NI_1n=1,\dots,Nk\geq 0k=\ell-n

I_1

I_2

J_1

N \to +\infty

[0,+\infty)f[0,+\infty)J_1J_2

J_1

J_11N/\left(2N+k\right)^2k=0,1,2,\dots

J_1

N\to +\infty

n2Nf[ 0, + \infty)

\displaystyle {\sum _{n=1}^{+\infty }{\frac {1}{n^{2}}}= {\frac {\pi ^{2}}{6}}}

m\geq 1

mm = 2\ell\ell(n,k)n \geqslant 1k\geqslant 0\ell = m/2mm = 2\ell+1\ell+1\ell = m/2+1/2

x\in \left(-\dfrac{1}{5},\dfrac{1}{5}\right)S=\dfrac{1}{1-5x}

\displaystyle x\in \bigcup_{k \in \mathbb{Z}}\left(\left( k-\dfrac 1 2 \right)\pi,k\pi\right)S=1-\dfrac{1}{\sin(2x)}

x\in \left(1,+\infty\right)S=\dfrac{1}{x-1}\{ a_n \}\subset \mathbb{R}\{ a_n \}

\{ a_n \}_{n \in \mathbb{N}}

\displaystyle \sum_{n=1}^{+\infty}a_n<+\infty

e^{x}= \exp(x)\quad \forall\, x \in \mathbb{R}

f:\mathbb{R} \to \mathbb{R}, \;f(x)=e^x\mathbb{R}\displaystyle\left\{ \prod_{k=1}^{n}\left(1+a_k\right) \right\}

\displaystyle \left\{ \prod_{k=1}^{n}\left(1+a_k\right) \right\}

n \geq 1

(1, +\infty)

y=1+x(0,1)

a_n >0n \geq 2

\displaystyle \sum_{n=2}^{+\infty}a_n

\left\{ a_n \right\}

n \geq 1

\alpha

HH\varepsilon=\dfrac{1}{2}N_{\frac{1}{2}}>0m>N_{\frac{1}{2}}p=m\geq0

H_{\alpha}\alpha \in (0,1). \varepsilon>0N>0m>Np\geq 0

p=m

H\alpha \in (0,1)

H_\alpha, \alpha>1\displaystyle H_n=\sum_{k=1}^{n} \dfrac{1}{k^\alpha}H_{n+1}\geq H_n\{ H_n \}\{ H_{2n+1} \}

\{ H_n \}\alpha >1Hf: [1,+\infty)\to \mathbb{R}, \; f(x) \coloneqq \dfrac{1}{x}

H_{\alpha}\alpha\neq 1\alpha> 0\,\,\wedge \alpha \neq 1 \left\{ \dfrac{1}{n^\alpha} \right\}H_\alphaf: [1,+\infty)\to \mathbb{R}, \; f(x)\coloneqq \dfrac{1}{x^\alpha}

H_{\alpha}

\alpha\in(1,+\infty)\alpha=1\alpha\in(-\infty,1)H

n \geq 1

H_{\alpha}\alpha\neq 1f: (0,+\infty)\to \mathbb{R}[1,+\infty)n\geq 1

[1,+\infty)

\beta\in\mathbb{R}\setminus \left\{ 0\right\}

(0,+\infty)

N \geq 21 \leq n \leq N

\alpha > 1

\alpha<1

\left\{ H_n \right\}

\left\{ H_n \right\}

\left\{ \ln n \right\}

\left\{ H_n \right\}\left\{ \ln n \right\}\left\{ H_n \right\}

\gamma

\left\{ \gamma_n \right\}n>1

\gamma_n \leq\gamma_{n-1}n>1

\left\{ \gamma_{n} \right\}\lfloor \cdot \rfloor : \mathbb{R} \to \mathbb{R}

[k,k+1)k \in \mathbb{Z}

\forall\, n \geq 1

\lfloor x \rfloor \leq xx \in \mathbb{R}\gamma \geq 0

y=1/x\gamma

n =1\left(\mathbb{N},\, \mathbb{Z},\, \mathbb{Q}\right)\mathbb{R}$

1. Prerequisiti di Analisi
   1. Ripasso algebra biennio liceo
   2. Ripasso geometria analitica
   3. Ripasso goniometria e trigonometria
   4. Errori tipici da evitare
   5. Insiemi numerici N,Z,Q,R
   6. Funzioni elementari
   7. Logica elementare
   8. Insiemi
2. Successioni
   1. Teoria sulle Successioni
   2. Estremo superiore e inferiore
   3. Limiti base
   4. Forme indeterminate
   5. Limiti notevoli
   6. Esercizi misti Successioni
   7. Successioni per ricorrenza
3. Funzioni
   1. Teoria sulle funzioni
   2. Verifica del limite in funzioni
   3. Limite base in funzioni
   4. Forme indeterminate in funzioni
   5. Limiti notevoli in funzioni
   6. Calcolo asintoti
   7. Studio di funzione senza derivate
   8. Dominio di una funzione
   9. Esercizi misti Funzioni
   10. Esercizi misti sui Limiti
4. Funzioni continue-lipschitziane-holderiane
   1. Teoria sulle Funzioni continue-lipschitziane-holderiane
   2. Continuità delle funzioni
   3. Continuità uniforme
   4. Teorema degli zeri
   5. Esercizi sul teorema di Weierstrass senza l’uso delle derivate
5. Calcolo differenziale
   1. Derivate
   2. Calcolo delle derivate
   3. Retta tangente nel calcolo differenziale
   4. Punti di non derivabilità nel calcolo differenziale
   5. Esercizi sul teorema di Weierstrass con l’uso delle derivate
   6. Studio di funzione completo nel calcolo differenziale
   7. Esercizi teorici nel calcolo differenziale
   8. Metodo di bisezione
   9. Metodo di Newton
6. Teoremi del calcolo differenziale
   1. Teoria sui Teoremi del calcolo differenziale
   2. Teorema di Rolle
   3. Teorema di Lagrange
   4. Teorema di Cauchy
   5. Teorema di De L’Hôpital
7. Calcolo integrale
   1. Integrale di Riemann
   2. Integrali immediati
   3. Integrale di funzione composta
   4. Integrali per sostituzione
   5. Integrali per parti
   6. Integrali di funzione razionale
   7. Calcolo delle aree
   8. Metodo dei rettangoli e dei trapezi
   9. Esercizi Misti Integrali Indefiniti
   10. Esercizi Misti Integrali Definiti
8. Integrali impropri
   1. Teoria Integrali impropri
   2. Carattere di un integrale improprio
   3. Calcolo di un integrale improprio
9. Espansione di Taylor
   1. Teoria Espansione di Taylor
   2. Limiti di funzione con Taylor
   3. Limiti di successione con Taylor
   4. Stime del resto
10. Funzioni integrali (Approfondimento)
    1. Teoria Funzioni integrali (Approfondimento)
    2. Studio di funzione integrale
    3. Limiti con Taylor e De L’Hôpital
    4. Derivazione di integrali parametrici (Tecnica di Feynmann)
11. Numeri Complessi
    1. Teoria Numeri complessi
    2. Espressioni con i numeri complessi
    3. Radice di un numero complesso
    4. Equazioni con i numeri complessi
    5. Disequazioni con i numeri complessi
    6. Esercizi misti Numeri complessi
12. Serie numeriche
    1. Teoria Serie numeriche
    2. Esercizi Serie a termini positivi
    3. Esercizi Serie a termini di segno variabile
    4. Esercizi Serie geometriche e telescopiche
13. Successioni di funzioni
    1. Teoria Successioni di funzioni
    2. Esercizi Successioni di funzioni
14. Serie di funzioni
    1. Teoria Serie di funzioni
    2. Esercizi Serie di funzioni
15. Serie di potenze
    1. Teoria Serie di potenze
    2. Esercizi Serie di potenze
16. Serie di Fourier
    1. Teoria Serie di Fourier
    2. Esercizi Serie di Fourier
17. Trasformata di Fourier
    1. Teoria Trasformata di Fourier
    2. Esercizi Trasformata di Fourier
18. Funzioni di più variabili
    1. Teoria Funzioni di più variabili
    2. Massimi e minimi liberi e vincolati
    3. Limiti in due variabili
    4. Integrali doppi
    5. Integrali tripli
    6. Integrali di linea di prima specie
    7. Integrali di linea di seconda specie
    8. Forme differenziali e campi vettoriali
    9. Teorema di Gauss-Green
    10. Integrali di superficie
    11. Flusso di un campo vettoriale
    12. Teorema di Stokes
    13. Teorema della divergenza
    14. Campi solenoidali
    15. Teorema del Dini
19. Equazioni differenziali lineari e non lineari
    1. Teoria equazioni differenziali lineari e non lineari
    2. Equazioni differenziali lineari e non lineari del primo ordine omogenee
20. Equazioni differenziali lineari
    1. Del primo ordine non omogenee
    2. Di ordine superiore al primo,a coefficienti costanti,omogenee
    3. Di ordine superiore al primo,a coefficienti costanti,non omogenee
    4. Di Eulero,di Bernoulli,di Clairaut,di Lagrange e di Abel
    5. Non omogenee avente per omogenea associata un’equazione di Eulero
    6. Sistemi di EDO
21. Equazioni differenziali non lineari
    1. A variabili separabiliO
    2. A secondo membro omogeneo
    3. Del tipo y’=y(ax+by+c)
    4. Del tipo y’=y(ax+by+c)/(a’x+b’y+c’)
    5. Equazioni differenziali esatte
    6. Mancanti delle variabili x e y
    7. Cenni sullo studio di un’assegnata equazione differenziale non lineare
    8. Di Riccati
    9. Cambi di variabile: simmetrie di Lie
22. Analisi complessa
    1. Fondamenti
    2. Funzioni olomorfe
    3. Integrale di Cauchy e applicazioni
    4. Teorema della curva di Jordan e teorema fondamentale dell’Algebra
    5. Teorema di inversione di Lagrange
    6. Teorema dei Residui
    7. Funzioni meromorfe
    8. Prodotti infiniti e prodotti di Weierstrass
    9. Continuazione analitica e topologia
    10. Teoremi di rigidità di funzioni olomorfe
    11. Trasformata di Mellin
23. Equazioni alle derivate parziali
    1. Equazioni del primo ordine
    2. Equazioni del secondo ordine lineari
    3. Equazioni non-lineari
    4. Sistemi di PDE
24. Funzioni speciali
    1. Funzione Gamma di Eulero
    2. Funzioni Beta,Digamma,Trigamma
    3. Integrali ellittici
    4. Funzioni di Bessel
    5. Funzione zeta di Riemann e funzioni L di Dirichlet
    6. Funzione polilogaritmo
    7. Funzioni ipergeometriche
25. Analisi funzionale
    1. Misura e integrale di Lebesgue
    2. Spazi Lp,teoremi di completezza e compattezza
    3. Spazi di Hilbert,serie e trasformata di Fourier
    4. Teoria e pratica dei polinomi ortogonali
    5. Spazi di Sobolev
26. Complementi
    1. Curiosità e approfondimenti
    2. Compiti di analisi
    3. Esercizi avanzati analisi
27. Funzioni Convesse

• Anelli.
• Gruppi.
• Campi.

• Sistemi lineari.
• Operazioni e proprieà.
• Applicazioni lineari e endomorfismi.
• Autovalori e diagonalizzazione.
• Forma canonica di Jordan e teorema spettrale.
• Spazi vettoriali.

• Geometria nel piano.
• Curve nel piano.
• Geometria nello spazio.
• Curve nello spazio.
• Superfici nello spazio in geometria analitica.
• Geometria affine.

• Curve nel piano e nello spazio.
• Superfici nello spazio in geometria differenziale.
• Varietà differenziabili.
• Tensori.
• Connessioni.
• Curvatura.

• Math Stack Exchange – Parte della rete Stack Exchange, questo sito è un forum di domande e risposte specificamente dedicato alla matematica. È una delle piattaforme più popolari per discutere e risolvere problemi matematici di vario livello, dall’elementare all’avanzato.
• Art of Problem Solving (AoPS) – Questo sito è molto noto tra gli studenti di matematica di livello avanzato e i partecipanti a competizioni matematiche. Offre forum, corsi online, e risorse educative su una vasta gamma di argomenti.
• MathOverflow – Questo sito è destinato a matematici professionisti e ricercatori. È una piattaforma per domande di ricerca avanzata in matematica. È strettamente legato a Math Stack Exchange ma è orientato a un pubblico con una formazione più avanzata.
• PlanetMath – Una comunità collaborativa di matematici che crea e cura articoli enciclopedici e altre risorse di matematica. È simile a Wikipedia, ma focalizzata esclusivamente sulla matematica.
• Wolfram MathWorld – Una delle risorse online più complete per la matematica. Contiene migliaia di articoli su argomenti di matematica, creati e curati da esperti. Sebbene non sia un forum, è una risorsa eccellente per la teoria matematica.
• The Math Forum – Un sito storico che offre un’ampia gamma di risorse, inclusi forum di discussione, articoli e risorse educative. Sebbene alcune parti del sito siano state integrate con altri servizi, come NCTM, rimane una risorsa preziosa per la comunità educativa.
• Stack Overflow (sezione matematica) – Sebbene Stack Overflow sia principalmente noto per la programmazione, ci sono anche discussioni rilevanti di matematica applicata, specialmente nel contesto della scienza dei dati, statistica, e algoritmi.
• Reddit (r/Math) – Un subreddit popolare dove si possono trovare discussioni su una vasta gamma di argomenti matematici. È meno formale rispetto ai siti di domande e risposte come Math Stack Exchange, ma ha una comunità attiva e molte discussioni interessanti.
• Brilliant.org – Offre corsi interattivi e problemi di matematica e scienza. È particolarmente utile per chi vuole allenare le proprie capacità di problem solving in matematica.
• Khan Academy – Una risorsa educativa globale con lezioni video, esercizi interattivi e articoli su una vasta gamma di argomenti di matematica, dalla scuola elementare all’università.